Too long; didn’t read

The formula for the starting term of a geometric sequence in a spreadsheet is:
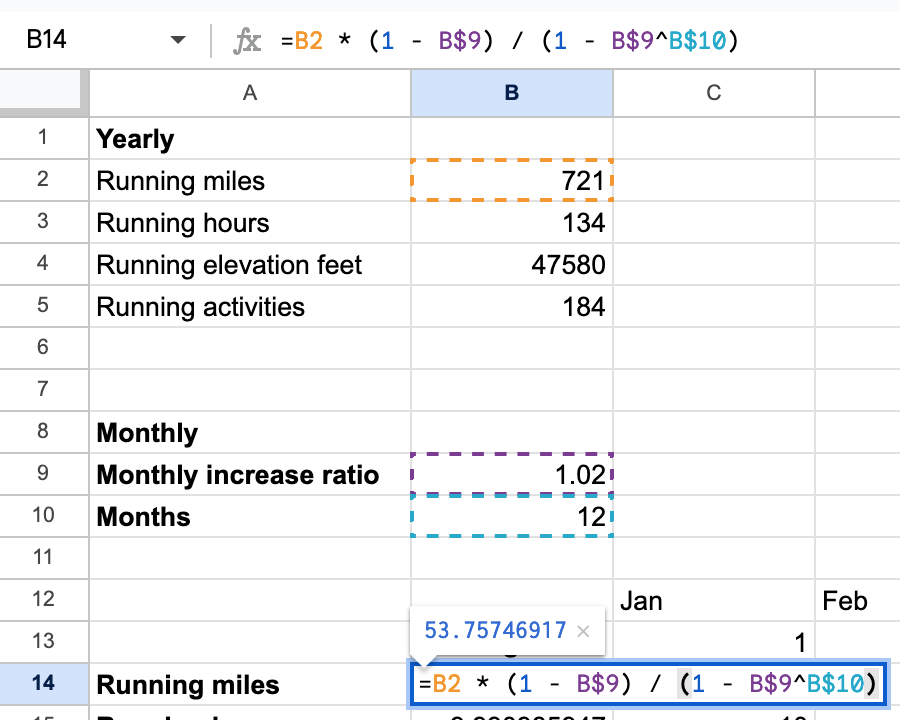
fx = B2 * (1 - B9) / (1 - B9^B10)

where B2 is the sum of the sequence, B9 is the common ratio, and B10 is the number of terms in the sequence.

How I got here

For my 2024 running goals, I set monthly goals based off of year-long goals but with a consistent month-to-month increase. For example, I have a goal to run 721 miles this year. My monthly goals start with 54 miles in January and increase by 2% (rounded) each month to 55 in February, 56 in March, 58, 59, 60, 61, 62, 63, 65, 66, and 67 miles in December.

I am not a mathematician, but I understand a sequence of numbers that change by fixed ratio is a geometric sequence. My initial thought was to increase by 10% each month, so my starting point was the total amount, the number of items in the sequence, and the ratio. I needed to calculate the starting number.

Of course, with this small a sample I could brute force it in the spreadsheet, but this is more fun.

I found some formulas on mathisfun.com. To calculate the value of an item in a geometric sequence, the formula is: $$x_n=a{r}^{(n-1)}$$

where $n$ is the index of the item in the sequence, $a$ is the first term, and $r$ is the common ratio. So if the sequence starts with $5$ and increases by $1.1$ (10%) for each term, we can calculate the 8th term with: $$\begin{array}{l}{x}_8=5\times {1.1}^{(8-1)}\\ x_8=5\times {1.1}^7\\ x_8=5\times 1.9487171\\ x_8=9.7435855\end{array}$$

And this is the formula to find the sum of a geometric sequence: $$\sum _{k=0}^{n-1}\left(a{r}^k\right)=a\left(\frac{1-r^n}{1-r}\right)$$

where $n$ is the number of terms to sum, $a$ is the first term, and $r$ is the common ratio.

With that formula, we can then solve for the first term, $a$: $$\begin{array}{c}\sum _{k=0}^{n-1}\left(a{r}^k\right)=a\left(\frac{1-r^n}{1-r}\right)\\ a\left(\frac{1-r^n}{1-r}\right)=\sum _{k=0}^{n-1}\left(a{r}^k\right)\\ a(1-r^n)=\sum _{k=0}^{n-1}\left(a{r}^k\right)(1-r)\\ a=\sum _{k=0}^{n-1}\left(a{r}^k\right)\left(\frac{1-r}{1-r^n}\right)\end{array}$$

Or, in a spreadsheet:
fx = B2 * (1 - B9) / (1 - B9^B10)

where B2 is the sum of the sequence, B9 is the common ratio, and B10 is the number of terms in the sequence. So for a goal of 721 miles over 12 months, with a monthly increase of 2%, my January running goal should be:
721 * (1 - 1.02) / (1 - 1.02^12) = 53.7574

I wrote that I wanted to increase by 10% each month, but my screenshot shows a 2% increase. After calculating everything for 10%, the end of the year was too overloaded and the start of the year was too underloaded. I finagled the ratio until the numbers looks more appropriate and landed on 2%.